2. MUSKINGUM CHANNEL ROUTING  METHODS

The Muskingum model was first developed by McCarthy (1938, cited by Mohan, 1997), for flood control studies in the Muskingum River basin in Ohio, USA. As perceived by Choudhury et al. (2002) and Singh and Woolhiser (2002), this method is still one of the most popular methods used for flood routing in several catchment models.

2.1 The Basic Muskingum Flood   Routing Method

Typically, the inflow hydrograph used in flood routing is derived by converting a measured stage into discharge using a steady state rating curve (Mutreja, 1986; Perumal and Raju, 1998; Moramarco and Singh, 2001).

As illustrated by Shaw (1994), storage in a river reach can be categorized into three forms, as depicted in Figure 2.1. During the rising stage of a flood in the reach, when inflow exceeds outflow, wedge storage must be added to prism storage. Conversely, during the falling stage, when inflow is less than outflow, wedge storage is negative and subtracted from prism storage to calculate total temporary storage in the reach. When outflow and inflow are equal in a reach, only prism storage is present in the channel.

Figure 2.1 Storage and non-steady flow (after Shaw, 1994).

Figure 2.2 illustrates an example of inflow and outflow hydrographs to and from a reach with prism storage. In a river reach characterized by a uniform cross-section and constant slope, velocity remains unchanged, indicating uniform flow (Chow, 1959). In these reaches, the peak of the outflow hydrograph aligns with the recession curve of the inflow hydrograph (Shaw, 1994).

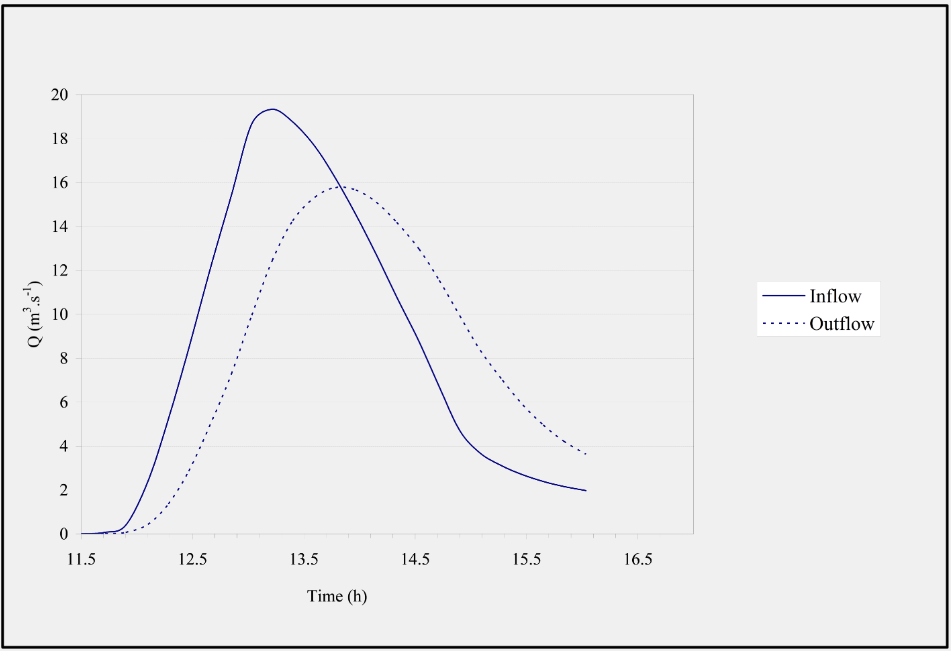
Figure 2.2 Example of inflow and outflow hydrographs.

According to Tung (1985) and Fread (1993), the most common form of the linear Muskingum model is expressed as the following equations:

where

where

When X = 0, Equation 2.3 simplifies to S_t = KQ_t, indicating that storage is solely dependent on outflow. When X = 0.5, equal weight is given to inflow and outflow, resulting in a condition akin to a uniformly progressive wave that does not attenuate (US Army Corps of Engineers, 1994a). Thus, 0.0 and 0.5 serve as limits for the value of X, determining the degree of attenuation of a flood wave within this range as it passes through the routing reach (US Army Corps of Engineers, 1994a).

Fread (1993) explained that an oversimplified depiction of unsteady flow along a routing reach may be seen as a lumped process, wherein the inflow at the upstream end and the outflow at the downstream end of the reach vary with time. In Muskingum flood routing, it is assumed that the storage in the system at any moment is proportionate to a weighted average of inflow and outflow from a given reach (Bauer, 1975).

According to the continuity equation (Equation 2.4), the rate of change of storage in a channel over time equals the difference between inflow and outflow (Shaw, 1994):

where

The combination and solution of Equations 2.3 and 2.4 in finite difference form yield the well-known Muskingum flow routing equations as presented in Equations 2.5 and 2.6.

Q_j+1^t+1 = C₀ I_j^t + C₁ I_j^t+1 + C₁I_j+1^t(2.5)

where

Qjt	=	outflow at time [t] of the jth sub-reach, and
Ijt	=	inflow at time [t] of the jth sub-reach.

The three coefficients (C₀, C₁, and C₂) are calculated as:

C₀ = (Δt + 2KX) / m (2.6a)

C₁ = (Δt - 2KX) / m (2.6b)

C₂ = (2K(1-X) - Δt) / m (2.6c)

m = 2K(1-X) + Δt (2.6d)

Here,C₀, C₁, and C₂ represent coefficients determined by functions of K, X, and a discretized time interval Δt. The sum of C₀, C₁, and C₂ equals one, so once C₀ and C₁ are calculated, C₂ can be derived as 1 - C₀ - C₁. Consequently, the outflow at the end of a time step is the weighted sum of the initial inflow and outflow, as well as the final inflow (Shaw, 1994). These three coefficients (C₀, C₁, and C₂) remain constant throughout the routing process (Fread, 1993).

As suggested by Viessman et al. (1989), it's important to avoid negative values for C₁. This is ensured when Equation 2.7 is satisfied. Negative values of C₂, however, do not impact the hydrographs routed during flooding (Viessman et al. , 1989).

Δt/K > 2X   (2.7)

where

K	=	change in time [s],
Ijt	=	the storage time constant for the river reach, which has a value close to the wave travel time within the river reach [s], and
X	=	a weighting factor varying between 0 and 0.5 [dimensionless].

After the X parameter is determined, the routing time interval should be checked again using the relationship shown in Figure 2.3 (Cunge, 1969; cited by NERC, 1975).

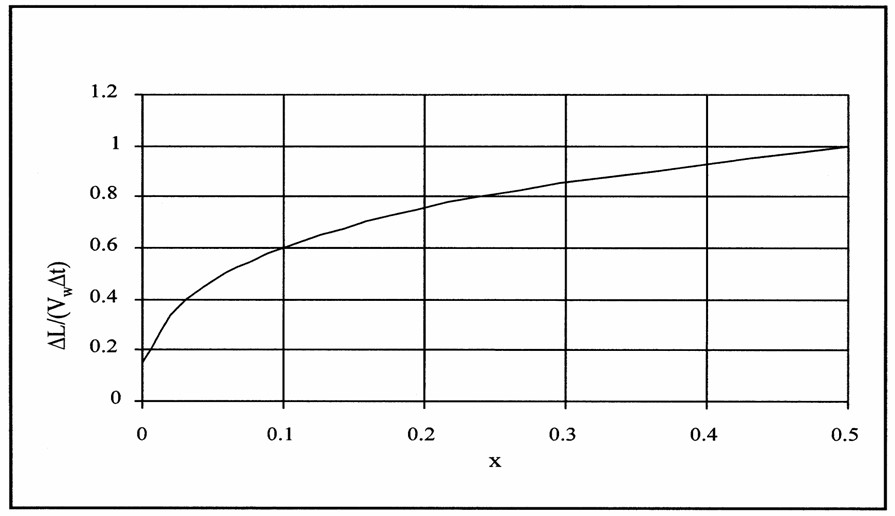
Figure 2.3 Cunge curve (Cunge, 1969 cited by NERC, 1975).

The time Δt is called the routing period and it must be chosen sufficiently small such that the assumption of flow rate linearity over time interval Δt is approximated (Gill, 1992). In particular, if Δt is too large, the peak of the inflow curve may be missed, so the period should be kept smaller than 1/5 of the travel time of the flood peak through the reach (Wilson, 1990). According to Viessman et al. (1989), theoretical stability of the numerical method is accomplished if Equation 2.8 is fulfilled:

2KX <= Δt <= 2K(1-X) (2.8)

Viessman et al. (1989) and Fread (1993) noted that the routing time interval (Δt) is frequently assigned any convenient value between the limits of (K/3) <= Δt <= K. Analysis of numerous flood waves suggests that the time taken for the flood wave's center of mass to traverse from the reach's upstream to downstream end equals K.(Viessman et al., 1989). The value of K can thus be estimated using gauged inflow and outflow data and with much greater ease and certainty than that of the X parameter (Viessman et al., 1989; Wilson, 1990). Among other factors in a catchment that influence the travel time (K), the most important are: drainage pattern, surface geology, soil type, catchment shape, and vegetal cover (Bauer and Midgley, 1974). None of these are readily expressible numerically, but to a large extent the factors are interdependent and can be generalized on a regional basis (Bauer and Midgley, 1974). Most researchers agree that the effectiveness of the Muskingum flood routing method depends on the accuracy of estimation of the K and X parameters (Singh and McCann, 1980; Wilson and Ruffin, 1988).

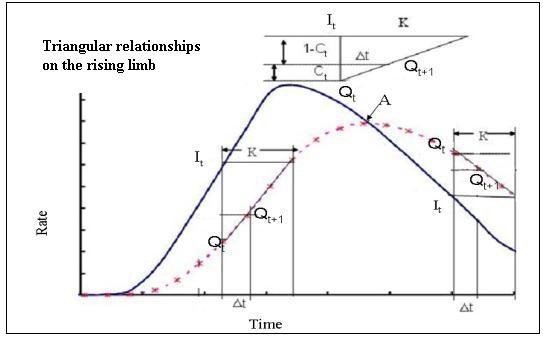
In order to determine the K and X parameters using observed inflow and outflow hydrographs, Equation 2.5 is used (Shaw, 1994). If observed inflow and outflow hydrographs are available for the reach, and When observed inflow and outflow hydrographs are accessible for the reach, and considering S_t and [XI_t + (1-X) Q_t] are assumed to be related via Equation 2.3, a graphical procedure to estimate K and X parameters may be implemented by assuming different values of X (Chow et al., 1988). The accepted value of X will then be that value of X that gives the best linear and narrowest loop (Gill, 1978; Fread, 1993). For example, in Figure 2.4, K is taken as the slope of the straight line of the narrowest loop X = 0.3 (Heggen, 1984). The shortcomings of the graphical method include the time required to construct the plots for alternative Xs, visual subjectivity, and the sensitivity of X in short reaches (Heggen, 1984; O'Donnell et al., 1988; Gelegenis and Sergio, 2000).

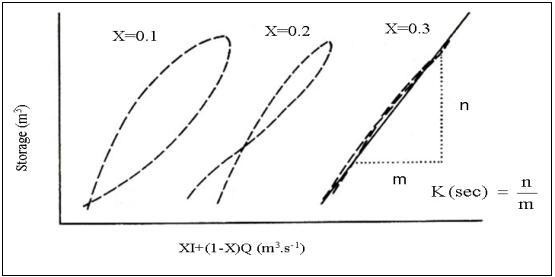
Figure 2.4 River routing storage loops (after Wilson, 1990).

The peak outflow does not lie on the inflow recession curve due to the effect of the wedge storage in streams (Shaw, 1994). As shown in Figure 2.5, the simulated outflow hydrograph is not a good reconstruction of the observed outflow. This discrepancy may arise when the relationships outlined in Equation 2.8, governing the interplay between K, X, and Δt, are not met (Gill, 1992).

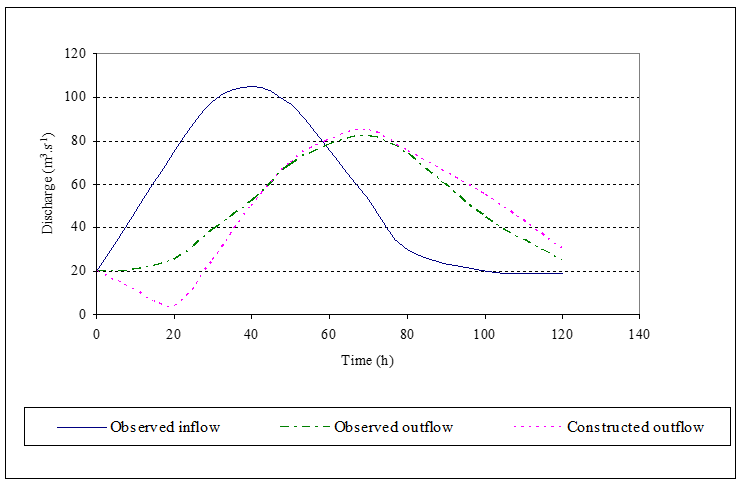
Figure 2.5 Muskingum routed hydrographs (after Shaw, 1994).

The basic Muskingum equation formulation is applicable to a single reach having no lateral inflow into the routing reach (Choudhury et al., 2002). In most rivers, this constrains the routing reaches to be rather short, generally terminating at tributaries, and requires gauged or estimated tributary inflows to be added to the main channel flow (O'Donnell, 1985). If there is lateral inflow in the form of substantial tributaries, the routing reaches may be chosen to terminate at a confluence, augmenting the main channel flow by the tributary flow for the next reach (O'Donnell, 1985). As explained by Fread (1993) and the US Army Corps of Engineers (1994a), the original Muskingum method is limited to moderate to slow rising hydrographs being routed through mild to steep sloping channels. The method is not applicable to steeply rising hydrographs such as dam breaks and ice breaks, where acceleration and momentum predominate, and the method neglects variable backwater effects such as downstream dams, constrictions, bridges and tidal influences (O'Donnell et al., 1988; Gelegenis and Sergio, 2000).

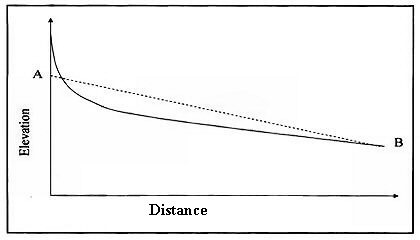
One of the disadvantages with hydrological methods of flow routing is that they assume a unique relationship between stage and discharge along the reach, even though the same discharge may have different flood levels at rising and falling stages (NERC, 1975). This phenomenon is indicated graphically in the well-known loop-rating curve as shown in Figure 2.6.

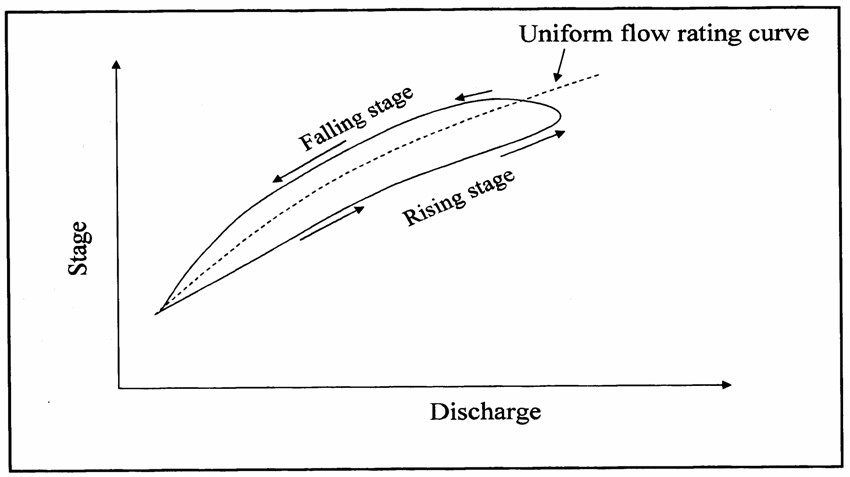
Figure 2.6 Loop-rating curve (after NERC, 1975).

2.2  The Muskingum Cunge Parameter     Estimation Method with Lateral Inflow

The original Muskingum method is based on the storage equation with the coefficients K and X derived by trial and error (O'Donnell et al., 1988; Gelegenis and Sergio, 2000). Unlike the basic Muskingum method where the parameters are calibrated based on observed stream flow data, in the Muskingum-Cunge method parameters are calculated based on flow and channel characteristics (Ponce, 1989). Hence, in the absence of observed flow data, the Muskingum-Cunge method may be used for parameter estimation (Smithers and Caldecott, 1993).

Equations 2.9 and 2.10 are used in the physically-based Muskingum-Cunge method to estimate the K and X parameters (Chow, 1959; Fread, 1993):

where

As seen in Equations 2.9 and 2.10, the Muskingum-Cunge K and X parameters are obtained using variables such as the top width of the river, wave celerity, reach cross-section area, reach length, and reach slope. The relation of the Muskingum K and X parameters to the catchment characteristics makes the Muskingum-Cunge method suitable for application to ungauged streams (Ponce, 1989). The Muskingum-Cunge method can simulate the celerity and diffusion of flood waves in a practical and accurate manner (Ponce and Yevjevich 1978; Ponce et al., 1996). The Muskingum flood routing models do not consider backwater effects, nor are they well suited for very mild sloping waterways where looped stage-discharge rating may exist (Fread, 1981; Feng and Xiaofang, 1999).

According to Wilson and Ruffin (1988), the reference discharge may be estimated as:

where

The kinematic wave celerity, defined as the slope of the discharge-area rating curve, may be estimated using Equation 2.12 (Chow, 1959):

where

In large catchments with lateral inflow to the main stream, the volume of the outflow hydrograph may exceed the inflow volume. Therefore, lateral inflow should be accounted for and added to the main flow as follows (NERC, 1975):

Equation 2.13 is an extension of Equation 2.5, once the K and X parameters are determined the C₀, C₁ and C₂ coefficients can be determined from Equation 2.6.

The C₃ coefficient, calculated using Equation 2.14, is added as a lateral inflow term in Equation 2.13 (NERC, 1975):

Flows associated with lateral inflow that are not routed in the main channel may be incorporated using Equations 2.14 and 2.15 (Fread, 1993). The total lateral flow per unit length is assumed to have a time distribution along the reach, specified at intervals of Δt (NERC, 1975). Backwater effects are disregarded, and lateral flows are assumed to enter proportionally along the main reach (Fread, 1993).

The Saint-Venant Equation for gradually varying flow in open channels is given as follows (NERC, 1975):

where

Fread (1998) approximated the terms in Equation 2.15a as:

where

Hence, lateral flow per unit (q) can be calculated from:

When the ratio of lateral inflow to the main flow is too large, numerical difficulties in solving Equation 2.15c may arise. Increasing the routing length (ΔL_j) of the specified reach may solve the numerical difficulties (Fread, 1993).

In channel routing, the travel time through a river reach may be larger than the routing interval Δt selected to meet the limits in Equation 2.8. When this occurs, the channel must be broken down into sub-reaches with smaller routing steps to simulate the flood wave movement and changes in hydrograph shape (US Army Corps of Engineers, 1994a). An initial estimate of the number of routing steps may be obtained by dividing the total travel time (K) by the routing interval time (Δt). According to the US Army Corps of Engineers (1994a), a general rule of thumb is that the computation interval should be less than 1/5 of the time of rise of the inflow hydrograph. As noted by Reed (1984), the space and time steps chosen should approximate Equation 2.16a:

Fread (1993) also suggested that the length can be estimated from Equation 2.16b.

2.3 The Three parameter Muskingum  Procedure  with Lateral Inflow

The Three parameter Muskingum procedure is a method based on the three-parameter Muskingum model, where the two conventional parameters are augmented by a third parameter to account for lateral inflow into the reach (O'Donnell et al., 1988). O'Donnell (1985)introduced a third parameter (α), assuming direct relationship between lateral inflow and main channel flow. Figure 2.7 illustrates the lateral inflow model. In the Three-parameter Muskingum method, the (α) parameter is multiplied by the stream inflow term and added as lateral inflow to the main flow, as shown in Equation 2.17:

Figure 2.7 Lateral inflow model (after O'Donnell et al., 1988).

In matrix formulation, the basic Muskingum routing Equation 2.5 may be written as (O'Donnell, 1985):

2.4 Application of the Three-parameter  Muskingum Model (Matrix)

In a study conducted on two British rivers, the Wye (75 km reach length) and the Wyre (25 km reach length), O'Donnell et al.(1988) demonstrated the dependency of the α parameter on individual flood events and recommended further studies to investigate α values in relation to storm rainfall distribution. The wide range of α values for different hydrographs implies radically different catchment drainage behavior and/or spatial storm distribution patterns. Other observations from the study include the following:

A possible reason for this difference in timing and magnitude is that the travel time for flood peaks is frequently much longer for out-of-bank events than for those within banks (O'Donnell et al., 1988). Additionally, for the three-parameter model fitted to each of the individual events, the reconstructed hydrographs' peak outflow was less than the observed peak values. In most cases, the timing of the reconstructed peak outflow was earlier than that of the observed one.

The following procedure is necessary to apply the three-parameter model (O'Donnell et al., 1988):

Application of the Three-parameter method requires observed inflow and outflow hydrographs to estimate the model parameters (K, X and α ) initially. The K, X, and α parameters of a catchment in the Three-parameter Muskingum method should be calibrated using different events needing many years of observed inflows and outflows hydrographs, since calibrating with specific events might give erroneous parameters for a given catchment (O'Donnell et al., 1988).

2.5 The Non-linear Muskingum Method

It is recognised that the storage versus weighted flow relationship is not always linear as is implied in Equation 2.3. If the relationship is non-linear, use of Equation 2.3 introduces considerable error (Gill, 1978).

Mohan (1997) proposed Equations 2.23 and 2.24, which utilise a non-linear Muskingum model in situations when the storage versus weighted flow relationship is non-linear:

where

Equations 2.23 and 2.24 have more degrees of freedom compared to Equation 2.3 and hence should yield a closer fit to the non-linear relation between storage and discharge. However, owing to the presence of non-linearity in the equation, the calibration procedure is complex (Gill, 1978; Mohan, 1997).

2.6 The SCS Convex Method

The US Soil Conservation Service (SCS) developed a coefficient channel routing technique similar to the Muskingum method. It has had widespread use in project planning and is used successfully even when limited storage data for the reach is available (Viessman et al., 1989).

The theory of the SCS Convex method is based on the following principle: when a flood passes through a natural stream that has negligible local inflows or transmission losses, there is a reach length (ΔL) and a time interval (Δt) such that discharge (Q_t+1) falls between inflow (I_t) and outflow (Q_t), as shown in Figure 2.8 (NRCS, 1972; Viessman et al., 1989). Equations 2.25 and 2.26 are algorithms for hydrograph rising and falling stages respectively (NRCS, 1972):

As explained by the NRCS (1972) and Viessman et al. (1989), the working equation for the Convex Method is derived from Figure 2.8. The total inflow and outflow volumes are equal; hence, the area under the inflow and outflow hydrographs are equal. The peak outflow is smaller and occurs later than the peak inflow and the curves cross at some point, A, as shown in Figure 2.8. This means that as Q_t+1 falls between I_t and Q_t at any time, the vertical distance of Q_t+1 above Q_t or below Q_t on the right hand side of A is a fraction (C_t) of the difference (I_t - Q_t), as shown in the inset of Figure 2.8. From triangle similarity relations, Equations 2.27 and 2.28 can be derived.

where

According to NRCS (1972) and Viessman et al. (1989), K is a constant storage parameter with time units and may be approximated from the Muskingum method. Similarly, C_t is approximately twice the Muskingum X.

Figure 2.8 Channel routing using the Convex method (after NRCS, 1972).

Equation 2.27 is thus a working equation to route the entire inflow hydrograph once C_t is established using Equation 2.28.

The Convex method of routing is valid only if C_t falls between 0.0 and 1.0 and, more importantly, Q_t+1 should always be between outflow Q_t and inflow I_t. The former can be controlled by selection of Δt, and the latter requirement is satisfied by the mathematical theory arising from analysis of convex sets (NRCS, 1972; Viessman et al., 1989).

Unlike other routing methods, the convex method equation for Q_t+1 is independent of I_t+1. Thus, the procedure can be used to forecast outflow from a reach without knowing the concurrent inflow. This provides a method for flood warning with a lead-time of at least the routing time Δt (Viessman et al., 1989).

2.7 Discharge and Channel  Relationships

As suggested by Clark and Davies (1988), rivers have a unique relationship between flow and channel dimensions, although close similarities are found for rivers in the same region with similar bed and bank materials and similar sediment loads. When there is limited data, relationships to relate channel dimensions to available variables are necessary. Of the many regime type equations that have been proposed, those relating channel width (b) to the dominant discharge have generally been found to be the most robust in application to rivers for which they were developed. These are mainly of the form as in Equation 2.29:

where

The coefficients z and m are estimated empirically. The values of z and m for various studies for gravel bed rivers are listed in Table 2.1.

Table 2.1 Coefficients of Equation 2.29 (after Clark and Davies, 1988).

Clark and Davies (1988) derived a relationship between slope and bankfull discharge for wadi channels in desert conditions given in Equation 2.30.

where

The relation between wetted perimeter (P) and discharge (Q) was developed for wide stable channels in Punjab, India by Lacey (1930, 1947, cited by Punmia and Pande, 1981). As noted by Klaassen and Vermeer (1988) and Garg (1992) the formula was applied in river schemes in part of India and Pakistan. Regime theory has been relatively successful in India and Pakistan in the design of stable irrigation channels under natural regimes (Savenije, 2003).

The Lacey equation is given by Lacey (1930, 1947; cited by Punmia and Pande, 1981), as

where

As suggested by Chow (1959), channel dimensions for the section factor shown in Equation 2.32a can be determined from a normal depth curve developed for rectangular, trapezoidal and circular sections as shown in Figure A.1 (Appendix A). For a given bottom width (b), the corresponding flow depth, area and hydraulic radius can be calculated from the curve.

where

Manning's equation is given as (Chow, 1959):

where

Equation 2.33 is an empirical relationship recommended by US Reclamation Service (Etcheverry, 1915, cited by Chow, 1959):

where

2.8 Flood Routing in Ungauged Rivers

As noted by the US Army Corps of Engineers (1994a), various flood runoff models have been developed based on the laws of thermodynamics and laws of conservation of mass, momentum and energy. Other models are empirical models which are numerical relationships derived from observed events. The Muskingum-Cunge routing model uses channel geometry, reach length, roughness coefficient, and slope to estimate the parameters of the model. Therefore, the Muskingum-Cunge method may be used for flood routing analysis in an ungauged catchment.

The problem of estimating flood magnitudes for ungauged catchments is one that arises frequently (Herbst, 1968). As explained by Kundzewicz (2002), ungauged catchments include catchments that are genuinely ungauged, poorly gauged, or those previously gauged and where monitoring has been discontinued. If there are no flow records from a catchment, methods that do not require the availability of observed hydrological record have to be used to estimate model parameters (Linsley et al., 1982).

According to the US Army Corps of Engineers (1994a), in channels with mild slopes and out of bank flows, X will be closer to 0.0. For steeper streams, with well-defined channels and flows within the banks, X will be closer to 0.5. Most natural channels lie somewhere in between these two limits.

2.9 Factors that Influence Flood  Routing

The factors influencing the practical application of the Muskingum flood routing method should be considered in parameter estimation techniques. Variables such as slope, backwater effect, and Manning roughness coefficient (n) have significant effects on flood routing applications. The following sections summarize these effects and limitations.

2.9.1 Slope

According to Manning's Equation (2.32b), changes in channel slope directly impact flow velocity, subsequently affecting lag time and hydrograph shape. Therefore, when applying flood routing techniques, these variables must be carefully considered to obtain reliable estimates of routing parameters.

Chow (1959), Fread (1993), and the US Army Corps of Engineers (1993) classify river slopes as mild, steep, or critical. A critical slope marks the point where a change in potential energy, rather than flow head, induces critical velocity. Slopes are considered mild when they are less than the critical slope and steep when greater. A negative slope indicates a downstream rise in the riverbed. Steady flow analysis is typically adequate for slopes exceeding 95 x10^-5 m/m. Flow conditions can further be classified based on the Froude number (defined in Equation 2.34) as subcritical, critical, or supercritical (Chow, 1959; Fread, 1993; US Army Corps of Engineers, 1993; Koegelenberg et al., 1997).

Froude number is estimated as follows,

where

The characteristic length (c) is commonly defined as the perpendicular cross-sectional area of the flow divided by the top width of the flow surface. The denominator term in Equation 2.34 represents the celerity of a shallow water wave (Fread, 1993; US Army Corps of Engineers, 1993).

The main slope of a channel is often determined using the simplest and most widely used method, as illustrated in Figure 2.9 (Linsley et al., 1988). In this method, the maximum elevation point is selected to derive a representative slope along the entire reach.

Figure 2.9 Mean stream slope (after Linsley et al., 1988).

Alternatively, conveyance slope measured at 10% and 85% of stream length from mouth of the river can be used (US Army Corps of Engineers, 1994a).

2.9.2 Backwater and inundation effects

Hydrological flood routing methods typically overlook variable backwater effects, such as downstream dams, constrictions, bridges, and tidal influences (O'Donnell, 1985). Moreover, as highlighted by the US Army Corps of Engineers (1993), these backwater effects significantly dampen flow dynamics, thereby challenging the linearity assumption in the Muskingum method.

2.9.3 Manning roughness coefficient

Roughness coefficients indicate the resistance to flood flows within channels and floodplains (Arcement and Schneider, 1989). As highlighted by Chow (1959) and Koegelenberg et al. (1997), there is no precise method for estimating roughness coefficients, making practical estimation of the Manning roughness coefficient subjective. These coefficients vary with flow depth and seasonal physical changes in riverbeds and banks. Therefore, design practices typically consider worst-case scenarios. Surface roughness, vegetation along the river, sediment load, channel irregularities, and wind blowing against the flow direction significantly influence resistance values. When there is minimal vegetation and irregularity just above the flow depth, resistance values decrease with increasing discharge (Chow, 1959; Arcement et al., 1989; Koegelenberg et al., 1997). Base roughness coefficient values (n_b) for different river conditions are listed in Table 2.2.

Table 2.2 Base roughness coefficient values (Arcement and Schneider, 1989) [Modified from Aldridge and Garret, 1973].

In selecting a base roughness coefficient (n) value for a channel, it must be classified as either a stable channel or a sand channel. A stable channel undergoes minimal changes throughout most of the inflow range (Arcement and Schneider, 1989).

Flow in a river may be confined to one or more channels, and during floods, it may occur in both the channel and the floodplain. The roughness coefficient (n) value is determined by factors affecting the roughness of channels and floodplains (Arcement and Schneider, 1989).

As noted by Shen and Julien (1993) and Fread (1993), the best results are achieved when the roughness coefficient (n) is calibrated against historical observations of stage and discharge. The Manning roughness coefficient (n) is also related to the Darcy friction factor f and the prevailing sediment size conditions of the bed materials, as shown in Equations 2.35 and 2.36 (Shen and Julien, 1993; Fread, 1993):

where

where

As demonstrated by Chow (1959), when applying the Manning formula to channels with composite roughness, it is sometimes necessary to compute an equivalent roughness coefficient value for the entire perimeter and use this value for the computation of flow throughout the entire section.

Limerinos (1970, cited by Arcement and Schneider, 1989) related the base roughness coefficient value to the hydraulic radius (R) and the particle size (d₈₄) of bed material ranging from small gravel to medium-sized boulders. Limerinos (1970) correlated n with the particle size having a minimum diameter equal to or exceeding the diameter of 84% of the particles, as shown in Equation 2.37:

where

Arcement and Schneider (1989), recommend Equation 2.37 to estimate the base roughness (n_b) value for a stable channel. The base roughness coefficient (n_b) values contained in Table 2.2 are for straight channels of nearly uniform cross-sectional shape. Hence, adjustments for channel irregularities, alignment, obstructions, vegetation, and meandering corrections may be made to account for particular channel characteristics using Equation 2.38 and the information contained in Table 2.3.

As noted by Arcement and Schneider (1989), projecting points or exposed trees increase the resistance coefficient. An increase of the resistance coefficient is also associated with a change in cross-sectional area.

The degree of meandering (m), depends on the ratio of the total length of the meandering channel in the reach being considered to the straight length of the channel reach (Arcement and Schneider, 1989).

Cowan (1956, cited by Chow, 1959), Arcement and Schneider (1989), and Land & Water Australia (2004) proposed that Manning's resistance value for open channel flow could be determined by considering all the factors that contribute to flow resistance. Hence, the value may be computed by considering all the channel characteristics as shown in Equation 2.38:

where

First, the river reach should be classified as a sand channel or stable channel. Then, the bed materials and the uniformity of the channel should be identified. Based on the channel type and characteristics, the base roughness value (n_b) is assigned from Table 2.2. Since the base value is for smooth and straight reaches, adjustments should be made using Table 2.3 to account for site conditions, including the degree of channel irregularity, variation in channel cross-section, effect of obstruction, amount of vegetation cover, and degree of meandering.

Table 2.3 Adjustment for channel roughness values (after Arcement and Schneider, 1989) [Modified from Aldridge and Garrett, 1973].

In this chapter the Muskingum flood routing methods, the relationship between discharge and channel, flood routing method applications in ungauged rivers, and factors that influence the practical application of flood routing methods have been discussed. In the next chapter, the catchment and event selection procedure will be detailed.